2.3 两个体系的比较
2.3.1 两个体系的分叉点
人类认知或说认识事物的第一步是识别或区分个体,因此我们需要考虑中西方两个认知体系在这一步是否已经开始分叉。因为亚氏逻辑学不研究对象或个体是如何来的,而这恰恰是我们比较的起点。所以在与《易经》比较时,需要在亚氏逻辑学方面添加一部分内容。
无论是西方的哲学、逻辑学和各个其它学科,都有一个共同的假设:存在一些与这些学科无关的、外在的、先验的、各自独立存在的个体,或者是客体、个体、物件等,称谓不同,含义基本相同。《易经》中太极生两仪是一个无中生有的过程,因此对应的西方概念很难找到。
《易经》的太极生两仪,两仪生四象过程,表述的是宇宙万物的运行演化规律,但同时也是我们对这个世界的一种认知,或者说是一种认知的表述。
当今的学术术语中,能够覆盖包括了思维、观察、知识、经验等不同领域的概念应当只有认知(cognition)。曾经作为人类最基本思维规律的逻辑,目前是作为一个基本的认知维度(cognitive dimension,其它维度还有哲学、心理学等)来看待的。
认知是一个很新的概念,外延和内涵都在发展中,对其含义的扩充也较为容易,因此这里就用这个概念来表述下面讨论的一些内容。我们这里引入这样一个假设:认知科学涵盖了对事物出现、产生的认知,或者说涵盖了识别出这些个体的任务。
在没有识别出某一类个体的第一个个体之前,无法确认存在这类个体,所以认知科学识别出第一个个体,类似于一种无中生有的过程。
把认知科学识别出个体的方式称之为划分,西方各门学科中一般可称之为划分出这个个体的内部和外部。这种划分出内外部的一分为二方式,与《易经》的太极生两仪类似,但又不相同。太极也可看作是一种划分规则,但是认为这个划分规则不是划分出一个个体内外两部分,而是划分出阴、阳两个部分,这两个部分之间具有相生的关系。
在做出这个从无到有的划分之后,接下来有两个不同的做法或选项:一个是进一步对划分出的阴阳两部分做同样的阴阳划分,另一个是寻找这第一个个体的同类个体,或者说用这个划分出来的个体去划分其他。前者可以说是进一步认识被认知对象的内部,可以用同样的划分规则;后者是以这个已经识别出的个体为基点,认识其他个体,或者说是认识这个个体的外部,在外部寻找与这个个体相同或相似之物。
能够识别一个个体的一般假设是:在不断地重复识别中,人们识别出的事物个体是可以完全或部分重复的。用信息论的术语说,人们可以得到的信息是有限的。
识别出的事物可以重复有两种基本情况:一种是识别出一些可重复出现的部分,另一种是观察到一些整体状态或现象的重复。
识别这些整体现象或状态时,能够获得重复的情况有两种,一种是如果这些整体的现象或状态数目是有限的,则可以通过有限次的认知识别出这些状态或现象,或者说得到有限的信息。另一种是不同的现象或状态间相似,变化不大,即使是有无限数目的现象或状态,如果是相似的状态或现象顺序出现,则识别过程也可得到有限的信息。
在认知科学识别出这些个体之后,其它学科再以这些个体为对象进行划分、分类,建立这些个体之间的关系等。这些学科的划分、分类方式与认知科学的识别方式不同。
当认为这个个体是完全已知的情况下,一般把这个个体称之为单元、元素、基本元素等。这个单元如何组成其它事物是进一步认知的任务。这种情况下,观察或识别这个单元如何组成其他事物,可以看作是对这个单元外部的认知。
总结上述讨论,在初始的一分为二划分之后,如何做下一步认知的两种选择导致了《易经》和西方逻辑认知的几个基本不同点:
其一,《易经》是同时考虑第一次划分出的两个部分,与此类推可以同时考虑四个、八个或六十四个部分。这也是一般称之为整体论、整体观的起点。亚氏逻辑学只考虑其中一个部分,把这个部分作为已知的单元来认识另一部分,就是万事从一开始。
其二,《易经》阴阳两者之间有特定的相生关系,这种关系是不变的,变化的是关系两端的个体。阴阳论直接用“阴、阳”这一对个体来表示其之间的关系,因此不必再造出一个新的关系个体。在西方的结构论中,是用了一个关系个体,因此还是从个体出发的。
其三,《易经》的阴阳相生,构成了一种循环。也正因此,构成了其可被认知的基础,即在一次次的认知中,可重复,可得到有限信息的认知结果。
当某类整体状态之间具有阴阳关系,且顺序出现的时候,就可称其为时间。如先把最小的自然时间单元“天”分为白天、夜晚,然后白天、夜晚还可以再一分为二;这个小的时间单元又嵌入在一个大的自然时间单元“月”中,月又可分为新月、残月两部分;月又嵌入在“年”这个时间单元中,古代中国一开始把年只分为冬夏两个季节(诗经中有:冬雷阵阵夏雨雪),后来分为春夏秋冬四季。
如前所述,这是一种循环嵌套的时间概念,与逐渐变化的绝对时间概念有本质的不同。实际上,这种循环嵌套的时间概念与日常生活中的时间概念更为一致,除了有日、月、年之外,根据星辰的周期变化还有更大范围的循环嵌套。
其四,被识别出的个体被其它学科作为对象,意味着这些学科会用自己的规则、方法来对这些对象分类,建立其间的关系等,而这些规则、方法与识别这些个体的认知无关,也就是与这些个体的产生、存在无关,因此就不得不引入一些假设,来判断这些个体存在的条件等,如本质属性假设等。那么如何认定这个本质属性,就成为一个基本问题。
《易经》没有这个问题。当用划分的观点看《易经》时,这个规则、道理和其所作的划分是相互定义,互“生”的,或者说是自定义的。没有规则做不出这个划分,反过来,没有这个划分的操作,这个规则、道理也显现不出来。“生”划分出了划分自身,即阳爻,把阳爻再生一次,就变成了阴爻,也就是阳爻一分为二,有了阴爻。第一次划分和后续的划分都基于同样的规则,因此对于《易经》来说,最初的认知和后续进一步的研究是统一的。
其五,西方的各个学科中,基本的划分规则是包含关系。这个包含关系是单向的,内部不能包含外部。《易经》的划分是阴阳相生的关系,是循环嵌套的。
其六,西方逻辑选择了渐进、线性的变化为其对象,是寻找相同和相似之物,使用的基本关系是BE、LIKE;《易经》的生,从无到有,从有到无,质变是其选择的对象。
亚氏逻辑学从哲学中分离出来之后,有了自己的论域。它不考虑逻辑学研究的对象是如何来的,它认为这些是其它学科的任务。它只研究对这些个体的表达、判断和推理。因此原子命题的真值/语义解释,在命题逻辑中无解。
对于亚氏逻辑学中的最基本问题——判断或命题的真值问题,或说语义(semantics)解释,在《易经》中不存在。究其原因,就在于《易经》涵盖了上述认知的第一、二步,因此《易经》的方法有着内生的语义解释或真值判断,或者说《易经》的卦象总是真的。用西方认识论的说法,《易经》叙述的内容就是知识。
上述亚氏逻辑学与《易经》的不同选择,导致了两种认知/认识路径。基于亚氏逻辑学的认知/认识路径是:从一个设定的起点,在一些可比较的路径中找到一条满意的路径,到达一个预期的终点。把这种认知/认识路径应用于概念获取,就会有应用最广泛的属种差定义方法:先假定有一个不可定义的概念,或称之为范畴,然后以这个范畴为属,加入其它种概念来定义其它概念,如此形成一个以范畴为根的概念树。
应用在推理中,则是是先设定存在一个前提,然后通过一系列的判断到达结论。应用到数学、物理、化学等具体的学科,则是先假定存在一组无法在本学科中证明的公理或定律,然后采用亚氏逻辑学的方式定义一组概念,推导出一系列定理,然后把这些概念和定理应用到分析实际问题,同时也验证这些公理、定律。
中国古代则是找到一个自相似的循环结构,先找到一个自相似局部或是一个循环节点,然后推算全局和整个的循环过程。
2.3.2 两个体系对数的处理
经典逻辑(数理逻辑)的四个组成部分之一,ZFC集合论建立以后,近乎成为整个数学的基础,完成了亚氏逻辑学与西方最成熟的符号体系——数学的融合。ZFC集合论承上启下,成为了亚氏逻辑学中的中枢。
相对于《易经》中爻、卦、生的内在自定义,构成ZFC集合论的是几个逻辑学以外的东西:客体、一个非逻辑二元关系∈和一组非逻辑公理(Non-logical axioms)。
ZFC公理系统引入的二元关系∈,部分类似于“生”,但是它与“生”的自定义不同,它由一组公理来刻画。ZFC公理系统其中之一是空集合存在公理:即存在一集合s,它没有元素。用朴素集合论的话说,即使没有隶属之物,隶属关系也存在。这类似于太极,空无一物中,有一个“生”的因素存在。
这个空集是第一个划分出的个体,但是一个非常特殊的个体,他没有内容之物,是个空的,因此不能进一步地划分。所以ZFC集合论从空集出发,定义自然数的方式,是以一种极限方式阐释了亚氏逻辑学的特点,另一方面这种极限情况也意味着其应用范围受到极大的约束。
约翰‧冯‧诺伊曼序数定义如下:
定义空集为零。
定义 n 的后继为 n ∪ {n}
它的一个特别性质,就是每个自然数 n 都是恰好含 n 个元素的集合,即{0,1,2,…,n-1}。这种从“空”(空集)生出的“有”(零)出发,整体上一步一步叠加,所构成的一个无穷自然数序列,意味着存在一种线性渐进的变化。无穷公理在确保所有自然数集合N存在的同时,也保证了在经历了无穷的变化之后,没有质的变化。在原有基础上的任何一个增量都不会改变性质,只是一种数量的增加。
有了自然数,也就有了实数,从而可以表示所有离散和连续的量,也就可表示所有可测量的现实对象。这种连续可测量的含义对应于一些诸如辐射生物效应中的线性无域假设,结构力学中的弹性区间等等。
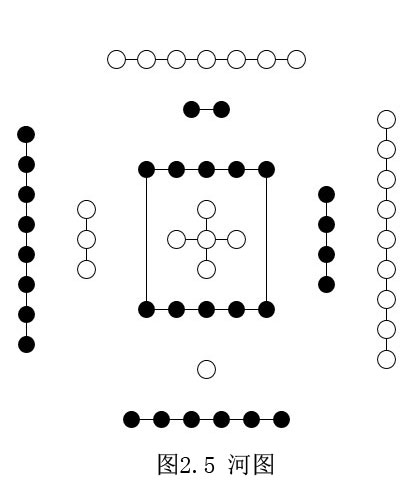
与ZF集合论定义自然数不同,河图揭示了自然数奇数(阳)、偶数(阴)之间的对应、互补、转化关系,表示了自然数的另外一种质变性质,表示阴极阳生,否极泰来的变化。
在十进制的九个个位数中,五个奇数为阳,五个偶数像阴。从一、二开始,相邻的两个奇、偶数为一对,两两相对表示阴阳相对。一、二和三、四两对阴阳在两个垂直的方向上,表示四象,六、七和八、九两对阴阳在另外一个层次上,与下面的四象叠加,成为八卦。表示了生老病死、成住坏灭等生死、坏灭的循环。
“五”单独一个,世界的中心、基础,出发点,像五行,与西方学说类似。一、二、三、四相对跳转一圈,回到中心的五;六、七、八、九也是相对的跳转一圈,回到中间的十(五加五),构成了另外一种次序。
所以说,河图应当包含了不止阴阳一种变化形式,伏羲根据河图制易,其易理可能不仅是根据周易流传下来的阴阳之易,还有其他的变化规律。
2.3.3《易经》、“顽固类”与分形
上面再讨论了《易经》与分形的关系后,下面再讨论一下与ZF集合论的关系。ZF集合论在排除了“顽固类”(类是个体的数学抽象)[程极泰,1985],也就是排除自身属于自身的情况后,为近代数学建立了一个稳固的基础,这一方面廓清了近代数学的论域,从而也廓清了引入近代数学的各门学科的疆域。
如果把由隶属关系定义集合看作是一个“生”成集合的过程,可以发现罗素悖论源于一个假设:在生成一个集合之前,这个集合已经存在了,因为只有一个集合在定义之前就存在,定义这个集合的属性为“包含了自身”才有意义。
根据罗素悖论,如果一个集合Sr的定义为满足隶属关系R,即:Sr = R(X),R的含义是所有不属于自身的集合X,都属于这个集合,而属于自身的集合,不属于这个集合。
即如果Sr = R(Sr)成立,那么就有Sr ≠ R(Sr),反之亦然,也就是产生了矛盾。
如果把这个判断看作是一个生成集合的过程,在生成集合之前,集合不存在,因此“不属于自身的集合”中就没有这个集合,即生成集合时,Sr ≠ R(Sr)。在生成了这个集合之后,这个集合尚不属于自身,那么我们就可以把这个隶属关系作用在自身之上,使得自身成为自身的元素,即Sr = R(R(X)) = R(R(Sr))成立。就是说,做这个判断的时候,关系R使用了两次的情况下,上述等式是存在的。
这个时候再做一次隶属判断,又会把自身排除出自身,也即:Sr ≠ R(R(R(Sr))),这个引用自身的判断我们可以一直继续下去,当R的数目为双数时,等式成立,单数时,不成立,也就是构成了一个无限循环隶属判断。这时候,属于和不属于两个类互斥而又相互依赖而存在,从一个类的存在,可以导出另一个类的存在,反之亦然,这也可以理解为一个类会嵌入自身。
这种互斥而又相互依从的类在我们周围是普遍存在的,如生死互斥,但是又相互依从。正负磁极互斥,又相互依从。上下、左右互斥,也都相互依存。并且这些都被当今各门学科看作是一些最基本的现象。
把类区分为“顽固类”和集合,顽固类对应于循环嵌套的结构,由上节的讨论可知,这也恰恰是《易经》研究的对象。
“顽固类”对应于一些不能独立存在的类,因此我们要对类的存在性做出一般性的讨论,或者说对抽象出类的个体的存在性,做出一般性讨论。下面我们把个体是否独立存在定义为:独立存在就是认知过程可独立识别这些个体,不独立存在就是识别一个个体时,还需要识别其他个体。如主、客体相互独立,认知过程将独立识别主体和客体。
识别这些相互依赖而存在的个体,既可以一次识别同时识别出所有这些相互依赖的个体,也可以认为是一个过程,即每次只识别一个个体,然后再依次识别依赖的个体。一次识别只识别一个个体,会识别出一个相互依赖的个体序列。如果这个序列一直延伸下去,并且永不重复,则不可能实现这个识别。反之有两种情况可以实现识别:一个是把这个序列截断在一点,认为存在一些不依赖于其它个体而存在的个体,从这个独立存在的个体开始,到当前要识别的个体结束,得到了一个有“方向”的个体序列。另一个就是存在一循环,如A依赖于B,B依赖于C,但是C又依赖于A,只要这个循环链条上的环节有限即可。
前一种情况的可独立存在个体可称之为基本个体,如物理学中的基本粒子,化学中的元素,逻辑学中的原子命题和范畴等。后一种情况引入了对识别过程的限制。把整体按照特定方式一次划分出多个相互依赖的个体,与循环识别一样都是受限制的识别。
把罗素悖论用于个体识别,可表述为:识别所有不识别自身的个体,不识别那些识别自身的个体。这种认知方式将导致循环识别。因此或者认可这种循环识别,或把对自身的识别排除在外,从而排除这种循环识别。如果把自身排除在外而识别的其它个体称之为客体,自身就称之为主体。
所以把罗素悖论引入个体识别,可导出主客体相互独立存在的哲学观点。主客体独立的假设排除了循环识别问题,顽固类作为一种个体也在排除之列,由此识别的个体对应于集合。那么顽固类对应的就是循环识别的个体,也是主客体不独立的个体。
认知主体和客体相互独立存在,主客体之间就没有内在的认知能力,需要外在的认知过程,这就是经验的含义。这种经验与主体、客体的存在无关,这时候与个体存在无关的逻辑学和数学就发挥了作用。
对于存在循环的识别过程,则无需有一个起点,因此不是从一个个体开始的认知,也无需区别主客体。在循环路径上的个体同时得到识别,其结果是一个认知识别过程同时识别一组个体,这些个体相互依赖而存在。相互依赖的个体背后是同一个整体,因此也是对这个整体内在的认知,这也是科学经验主义所排除的认知。
《易经》认为世界是一个整体,从一个完整一体的世界中,采用了一分为二、二分为四、四分为八的方式,从一个整体生出一组个体,可以看作是一次识别同时识别一组相互依赖的个体。逐层划分和识别出相互依存的个体,这也是给出了一种通用识别个体的认知方式。近代科学的各门学科均是采用一次识别一个个体的方式,这是与《易经》的一个根本区别。这也是一般把《易经》称之为整体论、整体观的来源。从另外一个角度看,就是形成了一组循环嵌套的个体,或者形成了这种“顽固类”对应的个体。
与近代科学找出连续的函数关系和概率不同,《易经》是找一个自相似的循环结构,先找到某一层次的自相似结构或是一个循环节点,然后推算其他层次的结构和整个的循环过程。这也是《易经》难以在近代被理解的基本原因。
《易经》的对象是被近代数学排除的“顽固类”,而《易经》又是一种分形,通过《易经》在顽固类和分形之间建立起了联系,因此可以讨论一下分形与顽固类的关系。
分形这个概念由法国/美国数学家本华·曼德博(法语:Benoît B. Mandelbrot)1975年首次提出。目前数学界对分形的定义仍存在争议,曼德博最初将分形总结为:“美丽、(研究起来)极其困难但又非常的有用,这就是分形。”1982年曼德博提出了更正式的定义:“分形是一种其豪斯多夫维数严格大于拓扑维数的集合。”后来他认为这种定义过于严格,于是简化并扩展了这个定义:“分形是由与整体在某些方面相似的部分构成的图形。”又过了一段时间,曼德博决定使用以下方式来描述分形:“……在研究和使用分形时,不需要迂腐的定义。用分形维数作为描述各种不同分型的通用术语。”
分形一般有以下特质:
在任意小的尺度上都能有精细的结构;
太不规则,以至无论是其整体或局部都难以用传统欧氏几何的语言来描述;
具有(至少是近似的或统计的)自相似形式;
一般地,其“分形维数”(通常为豪斯多夫维数)会大于拓扑维数(但在空间填充曲线如希尔伯特曲线中为例外);
在多数情况下有着简单的递归定义。
从数学的角度讲,分形的性质有:
无标度性或标度不变性;
作为一个数学函数,分形通常是处处不可微的;
分数维数;
在多数情况下有着简单的递归定义。
对比分形的这些特征和上述对顽固类的讨论,分形符合顽固类的定义,简单地讲,分形就是一种顽固类的实例,而顽固类是分形的数学含义。
这也就可以理解,为什么至今为止无法给出分形的一个合适的定义,原因就在于分形已经被ZF集合论排除在外,因此也被近代数学的基础理论排除在外。(待续)
──转自《大纪元》
(责任编辑:李敏)