2.3 兩個體系的比較
2.3.1 兩個體系的分叉點
人類認知或說認識事物的第一步是識別或區分個體,因此我們需要考慮中西方兩個認知體系在這一步是否已經開始分叉。因為亞氏邏輯學不研究對象或個體是如何來的,而這恰恰是我們比較的起點。所以在與《易經》比較時,需要在亞氏邏輯學方面添加一部分內容。
無論是西方的哲學、邏輯學和各個其它學科,都有一個共同的假設:存在一些與這些學科無關的、外在的、先驗的、各自獨立存在的個體,或者是客體、個體、物件等,稱謂不同,含義基本相同。《易經》中太極生兩儀是一個無中生有的過程,因此對應的西方概念很難找到。
《易經》的太極生兩儀,兩儀生四象過程,表述的是宇宙萬物的運行演化規律,但同時也是我們對這個世界的一種認知,或者說是一種認知的表述。
當今的學術術語中,能夠覆蓋包括了思維、觀察、知識、經驗等不同領域的概念應當只有認知(cognition)。曾經作為人類最基本思維規律的邏輯,目前是作為一個基本的認知維度(cognitive dimension,其它維度還有哲學、心理學等)來看待的。
認知是一個很新的概念,外延和內涵都在發展中,對其含義的擴充也較為容易,因此這裡就用這個概念來表述下面討論的一些內容。我們這裡引入這樣一個假設:認知科學涵蓋了對事物出現、產生的認知,或者說涵蓋了識別出這些個體的任務。
在沒有識別出某一類個體的第一個個體之前,無法確認存在這類個體,所以認知科學識別出第一個個體,類似於一種無中生有的過程。
把認知科學識別出個體的方式稱之為劃分,西方各門學科中一般可稱之為劃分出這個個體的內部和外部。這種劃分出內外部的一分為二方式,與《易經》的太極生兩儀類似,但又不相同。太極也可看作是一種劃分規則,但是認為這個劃分規則不是劃分出一個個體內外兩部分,而是劃分出陰、陽兩個部分,這兩個部分之間具有相生的關係。
在做出這個從無到有的劃分之後,接下來有兩個不同的做法或選項:一個是進一步對劃分出的陰陽兩部分做同樣的陰陽劃分,另一個是尋找這第一個個體的同類個體,或者說用這個劃分出來的個體去劃分其他。前者可以說是進一步認識被認知對象的內部,可以用同樣的劃分規則;後者是以這個已經識別出的個體為基點,認識其他個體,或者說是認識這個個體的外部,在外部尋找與這個個體相同或相似之物。
能夠識別一個個體的一般假設是:在不斷地重複識別中,人們識別出的事物個體是可以完全或部分重複的。用信息論的術語說,人們可以得到的信息是有限的。
識別出的事物可以重複有兩種基本情況:一種是識別出一些可重複出現的部分,另一種是觀察到一些整體狀態或現象的重複。
識別這些整體現象或狀態時,能夠獲得重複的情況有兩種,一種是如果這些整體的現象或狀態數目是有限的,則可以通過有限次的認知識別出這些狀態或現象,或者說得到有限的信息。另一種是不同的現象或狀態間相似,變化不大,即使是有無限數目的現象或狀態,如果是相似的狀態或現象順序出現,則識別過程也可得到有限的信息。
在認知科學識別出這些個體之後,其它學科再以這些個體為對象進行劃分、分類,建立這些個體之間的關係等。這些學科的劃分、分類方式與認知科學的識別方式不同。
當認為這個個體是完全已知的情況下,一般把這個個體稱之為單元、元素、基本元素等。這個單元如何組成其它事物是進一步認知的任務。這種情況下,觀察或識別這個單元如何組成其他事物,可以看作是對這個單元外部的認知。
總結上述討論,在初始的一分為二劃分之後,如何做下一步認知的兩種選擇導致了《易經》和西方邏輯認知的幾個基本不同點:
其一,《易經》是同時考慮第一次劃分出的兩個部分,與此類推可以同時考慮四個、八個或六十四個部分。這也是一般稱之為整體論、整體觀的起點。亞氏邏輯學只考慮其中一個部分,把這個部分作為已知的單元來認識另一部分,就是萬事從一開始。
其二,《易經》陰陽兩者之間有特定的相生關係,這種關係是不變的,變化的是關係兩端的個體。陰陽論直接用「陰、陽」這一對個體來表示其之間的關係,因此不必再造出一個新的關係個體。在西方的結構論中,是用了一個關係個體,因此還是從個體出發的。
其三,《易經》的陰陽相生,構成了一種循環。也正因此,構成了其可被認知的基礎,即在一次次的認知中,可重複,可得到有限信息的認知結果。
當某類整體狀態之間具有陰陽關係,且順序出現的時候,就可稱其為時間。如先把最小的自然時間單元「天」分為白天、夜晚,然後白天、夜晚還可以再一分為二;這個小的時間單元又嵌入在一個大的自然時間單元「月」中,月又可分為新月、殘月兩部分;月又嵌入在「年」這個時間單元中,古代中國一開始把年只分為冬夏兩個季節(詩經中有:冬雷陣陣夏雨雪),後來分為春夏秋冬四季。
如前所述,這是一種循環嵌套的時間概念,與逐漸變化的絕對時間概念有本質的不同。實際上,這種循環嵌套的時間概念與日常生活中的時間概念更為一致,除了有日、月、年之外,根據星辰的周期變化還有更大範圍的循環嵌套。
其四,被識別出的個體被其它學科作為對象,意味著這些學科會用自己的規則、方法來對這些對象分類,建立其間的關係等,而這些規則、方法與識別這些個體的認知無關,也就是與這些個體的產生、存在無關,因此就不得不引入一些假設,來判斷這些個體存在的條件等,如本質屬性假設等。那麼如何認定這個本質屬性,就成為一個基本問題。
《易經》沒有這個問題。當用劃分的觀點看《易經》時,這個規則、道理和其所作的劃分是相互定義,互「生」的,或者說是自定義的。沒有規則做不出這個劃分,反過來,沒有這個劃分的操作,這個規則、道理也顯現不出來。「生」劃分出了劃分自身,即陽爻,把陽爻再生一次,就變成了陰爻,也就是陽爻一分為二,有了陰爻。第一次劃分和後續的劃分都基於同樣的規則,因此對於《易經》來說,最初的認知和後續進一步的研究是統一的。
其五,西方的各個學科中,基本的劃分規則是包含關係。這個包含關係是單向的,內部不能包含外部。《易經》的劃分是陰陽相生的關係,是循環嵌套的。
其六,西方邏輯選擇了漸進、線性的變化為其對象,是尋找相同和相似之物,使用的基本關係是BE、LIKE;《易經》的生,從無到有,從有到無,質變是其選擇的對象。
亞氏邏輯學從哲學中分離出來之後,有了自己的論域。它不考慮邏輯學研究的對象是如何來的,它認為這些是其它學科的任務。它只研究對這些個體的表達、判斷和推理。因此原子命題的真值/語義解釋,在命題邏輯中無解。
對於亞氏邏輯學中的最基本問題——判斷或命題的真值問題,或說語義(semantics)解釋,在《易經》中不存在。究其原因,就在於《易經》涵蓋了上述認知的第一、二步,因此《易經》的方法有著內生的語義解釋或真值判斷,或者說《易經》的卦象總是真的。用西方認識論的說法,《易經》敘述的內容就是知識。
上述亞氏邏輯學與《易經》的不同選擇,導致了兩種認知/認識路徑。基於亞氏邏輯學的認知/認識路徑是:從一個設定的起點,在一些可比較的路徑中找到一條滿意的路徑,到達一個預期的終點。把這種認知/認識路徑應用於概念獲取,就會有應用最廣泛的屬種差定義方法:先假定有一個不可定義的概念,或稱之為範疇,然後以這個範疇為屬,加入其它種概念來定義其它概念,如此形成一個以範疇為根的概念樹。
應用在推理中,則是是先設定存在一個前提,然後通過一系列的判斷到達結論。應用到數學、物理、化學等具體的學科,則是先假定存在一組無法在本學科中證明的公理或定律,然後採用亞氏邏輯學的方式定義一組概念,推導出一系列定理,然後把這些概念和定理應用到分析實際問題,同時也驗證這些公理、定律。
中國古代則是找到一個自相似的循環結構,先找到一個自相似局部或是一個循環節點,然後推算全局和整個的循環過程。
2.3.2 兩個體系對數的處理
經典邏輯(數理邏輯)的四個組成部分之一,ZFC集合論建立以後,近乎成為整個數學的基礎,完成了亞氏邏輯學與西方最成熟的符號體系——數學的融合。ZFC集合論承上啟下,成為了亞氏邏輯學中的中樞。
相對於《易經》中爻、卦、生的內在自定義,構成ZFC集合論的是幾個邏輯學以外的東西:客體、一個非邏輯二元關係∈和一組非邏輯公理(Non-logical axioms)。
ZFC公理系統引入的二元關係∈,部分類似於「生」,但是它與「生」的自定義不同,它由一組公理來刻畫。ZFC公理系統其中之一是空集合存在公理:即存在一集合s,它沒有元素。用樸素集合論的話說,即使沒有隸屬之物,隸屬關係也存在。這類似於太極,空無一物中,有一個「生」的因素存在。
這個空集是第一個劃分出的個體,但是一個非常特殊的個體,他沒有內容之物,是個空的,因此不能進一步地劃分。所以ZFC集合論從空集出發,定義自然數的方式,是以一種極限方式闡釋了亞氏邏輯學的特點,另一方面這種極限情況也意味著其應用範圍受到極大的約束。
約翰‧馮‧諾伊曼序數定義如下:
定義空集為零。
定義 n 的後繼為 n ∪ {n}
它的一個特別性質,就是每個自然數 n 都是恰好含 n 個元素的集合,即{0,1,2,…,n-1}。這種從「空」(空集)生出的「有」(零)出發,整體上一步一步疊加,所構成的一個無窮自然數序列,意味著存在一種線性漸進的變化。無窮公理在確保所有自然數集合N存在的同時,也保證了在經歷了無窮的變化之後,沒有質的變化。在原有基礎上的任何一個增量都不會改變性質,只是一種數量的增加。
有了自然數,也就有了實數,從而可以表示所有離散和連續的量,也就可表示所有可測量的現實對象。這種連續可測量的含義對應於一些諸如輻射生物效應中的線性無域假設,結構力學中的彈性區間等等。
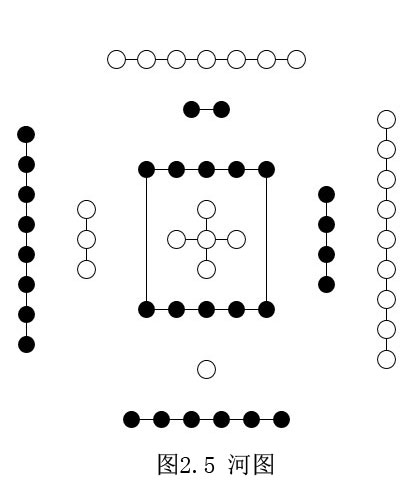
與ZF集合論定義自然數不同,河圖揭示了自然數奇數(陽)、偶數(陰)之間的對應、互補、轉化關係,表示了自然數的另外一種質變性質,表示陰極陽生,否極泰來的變化。
在十進制的九個個位數中,五個奇數為陽,五個偶數像陰。從一、二開始,相鄰的兩個奇、偶數為一對,兩兩相對表示陰陽相對。一、二和三、四兩對陰陽在兩個垂直的方向上,表示四象,六、七和八、九兩對陰陽在另外一個層次上,與下面的四象疊加,成為八卦。表示了生老病死、成住壞滅等生死、壞滅的循環。
「五」單獨一個,世界的中心、基礎,出發點,像五行,與西方學說類似。一、二、三、四相對跳轉一圈,回到中心的五;六、七、八、九也是相對的跳轉一圈,回到中間的十(五加五),構成了另外一種次序。
所以說,河圖應當包含了不止陰陽一種變化形式,伏羲根據河圖制易,其易理可能不僅是根據周易流傳下來的陰陽之易,還有其他的變化規律。
2.3.3《易經》、「頑固類」與分形
上面再討論了《易經》與分形的關係後,下面再討論一下與ZF集合論的關係。ZF集合論在排除了「頑固類」(類是個體的數學抽象)[程極泰,1985],也就是排除自身屬於自身的情況後,為近代數學建立了一個穩固的基礎,這一方面廓清了近代數學的論域,從而也廓清了引入近代數學的各門學科的疆域。
如果把由隸屬關係定義集合看作是一個「生」成集合的過程,可以發現羅素悖論源於一個假設:在生成一個集合之前,這個集合已經存在了,因為只有一個集合在定義之前就存在,定義這個集合的屬性為「包含了自身」才有意義。
根據羅素悖論,如果一個集合Sr的定義為滿足隸屬關係R,即:Sr = R(X),R的含義是所有不屬於自身的集合X,都屬於這個集合,而屬於自身的集合,不屬於這個集合。
即如果Sr = R(Sr)成立,那麼就有Sr ≠ R(Sr),反之亦然,也就是產生了矛盾。
如果把這個判斷看作是一個生成集合的過程,在生成集合之前,集合不存在,因此「不屬於自身的集合」中就沒有這個集合,即生成集合時,Sr ≠ R(Sr)。在生成了這個集合之後,這個集合尚不屬於自身,那麼我們就可以把這個隸屬關係作用在自身之上,使得自身成為自身的元素,即Sr = R(R(X)) = R(R(Sr))成立。就是說,做這個判斷的時候,關係R使用了兩次的情況下,上述等式是存在的。
這個時候再做一次隸屬判斷,又會把自身排除出自身,也即:Sr ≠ R(R(R(Sr))),這個引用自身的判斷我們可以一直繼續下去,當R的數目為雙數時,等式成立,單數時,不成立,也就是構成了一個無限循環隸屬判斷。這時候,屬於和不屬於兩個類互斥而又相互依賴而存在,從一個類的存在,可以導出另一個類的存在,反之亦然,這也可以理解為一個類會嵌入自身。
這種互斥而又相互依從的類在我們周圍是普遍存在的,如生死互斥,但是又相互依從。正負磁極互斥,又相互依從。上下、左右互斥,也都相互依存。並且這些都被當今各門學科看作是一些最基本的現象。
把類區分為「頑固類」和集合,頑固類對應於循環嵌套的結構,由上節的討論可知,這也恰恰是《易經》研究的對象。
「頑固類」對應於一些不能獨立存在的類,因此我們要對類的存在性做出一般性的討論,或者說對抽象出類的個體的存在性,做出一般性討論。下面我們把個體是否獨立存在定義為:獨立存在就是認知過程可獨立識別這些個體,不獨立存在就是識別一個個體時,還需要識別其他個體。如主、客體相互獨立,認知過程將獨立識別主體和客體。
識別這些相互依賴而存在的個體,既可以一次識別同時識別出所有這些相互依賴的個體,也可以認為是一個過程,即每次只識別一個個體,然後再依次識別依賴的個體。一次識別只識別一個個體,會識別出一個相互依賴的個體序列。如果這個序列一直延伸下去,並且永不重複,則不可能實現這個識別。反之有兩種情況可以實現識別:一個是把這個序列截斷在一點,認為存在一些不依賴於其它個體而存在的個體,從這個獨立存在的個體開始,到當前要識別的個體結束,得到了一個有「方向」的個體序列。另一個就是存在一循環,如A依賴於B,B依賴於C,但是C又依賴於A,只要這個循環鏈條上的環節有限即可。
前一種情況的可獨立存在個體可稱之為基本個體,如物理學中的基本粒子,化學中的元素,邏輯學中的原子命題和範疇等。後一種情況引入了對識別過程的限制。把整體按照特定方式一次劃分出多個相互依賴的個體,與循環識別一樣都是受限制的識別。
把羅素悖論用於個體識別,可表述為:識別所有不識別自身的個體,不識別那些識別自身的個體。這種認知方式將導致循環識別。因此或者認可這種循環識別,或把對自身的識別排除在外,從而排除這種循環識別。如果把自身排除在外而識別的其它個體稱之為客體,自身就稱之為主體。
所以把羅素悖論引入個體識別,可導出主客體相互獨立存在的哲學觀點。主客體獨立的假設排除了循環識別問題,頑固類作為一種個體也在排除之列,由此識別的個體對應於集合。那麼頑固類對應的就是循環識別的個體,也是主客體不獨立的個體。
認知主體和客體相互獨立存在,主客體之間就沒有內在的認知能力,需要外在的認知過程,這就是經驗的含義。這種經驗與主體、客體的存在無關,這時候與個體存在無關的邏輯學和數學就發揮了作用。
對於存在循環的識別過程,則無需有一個起點,因此不是從一個個體開始的認知,也無需區別主客體。在循環路徑上的個體同時得到識別,其結果是一個認知識別過程同時識別一組個體,這些個體相互依賴而存在。相互依賴的個體背後是同一個整體,因此也是對這個整體內在的認知,這也是科學經驗主義所排除的認知。
《易經》認為世界是一個整體,從一個完整一體的世界中,採用了一分為二、二分為四、四分為八的方式,從一個整體生出一組個體,可以看作是一次識別同時識別一組相互依賴的個體。逐層劃分和識別出相互依存的個體,這也是給出了一種通用識別個體的認知方式。近代科學的各門學科均是採用一次識別一個個體的方式,這是與《易經》的一個根本區別。這也是一般把《易經》稱之為整體論、整體觀的來源。從另外一個角度看,就是形成了一組循環嵌套的個體,或者形成了這種「頑固類」對應的個體。
與近代科學找出連續的函數關係和概率不同,《易經》是找一個自相似的循環結構,先找到某一層次的自相似結構或是一個循環節點,然後推算其他層次的結構和整個的循環過程。這也是《易經》難以在近代被理解的基本原因。
《易經》的對象是被近代數學排除的「頑固類」,而《易經》又是一種分形,通過《易經》在頑固類和分形之間建立起了聯繫,因此可以討論一下分形與頑固類的關係。
分形這個概念由法國/美國數學家本華·曼德博(法語:Benoît B. Mandelbrot)1975年首次提出。目前數學界對分形的定義仍存在爭議,曼德博最初將分形總結為:「美麗、(研究起來)極其困難但又非常的有用,這就是分形。」1982年曼德博提出了更正式的定義:「分形是一種其豪斯多夫維數嚴格大於拓撲維數的集合。」後來他認為這種定義過於嚴格,於是簡化並擴展了這個定義:「分形是由與整體在某些方面相似的部分構成的圖形。」又過了一段時間,曼德博決定使用以下方式來描述分形:「……在研究和使用分形時,不需要迂腐的定義。用分形維數作為描述各種不同分型的通用術語。」
分形一般有以下特質:
在任意小的尺度上都能有精細的結構;
太不規則,以至無論是其整體或局部都難以用傳統歐氏幾何的語言來描述;
具有(至少是近似的或統計的)自相似形式;
一般地,其「分形維數」(通常為豪斯多夫維數)會大於拓撲維數(但在空間填充曲線如希爾伯特曲線中為例外);
在多數情況下有著簡單的遞歸定義。
從數學的角度講,分形的性質有:
無標度性或標度不變性;
作為一個數學函數,分形通常是處處不可微的;
分數維數;
在多數情況下有著簡單的遞歸定義。
對比分形的這些特徵和上述對頑固類的討論,分形符合頑固類的定義,簡單地講,分形就是一種頑固類的實例,而頑固類是分形的數學含義。
這也就可以理解,為什麼至今為止無法給出分形的一個合適的定義,原因就在於分形已經被ZF集合論排除在外,因此也被近代數學的基礎理論排除在外。(待續)
──轉自《大紀元》
(責任編輯:李敏)






























